La gaussiana normalizzata ha equazione:
![]()
Essa ha simmetria proprio nel valor medio ![]() .
.
Il suo grafico varia al variare della deviazione standard. Questa figura chiarisce il concetto:
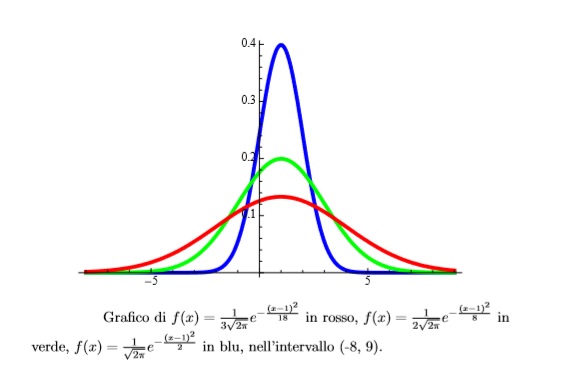
Essa è una densità di probabilità ed effettuando la sua integrazione trovo proprio la distribuzione di probabilità che fornisce la probabilità che un evento possa accadere in un intervallo.
In pratica:
![]()
Il calcolo di questo integrale non è banale e si preferisce calcolare l’integrale della stessa curva ma traslata nell’origine, standardizzandola ,ponendo:
![]()
La gaussiana normalizzata standard avrà equazione:
![]()
con media nulla ossia ![]() e deviazione standard unitaria
e deviazione standard unitaria ![]()
Questo disegno chiarisce la cosa:
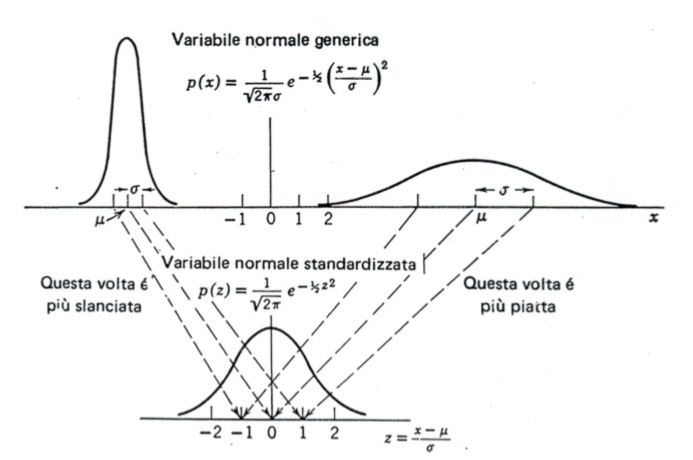
In generale:
![]()
e per calcolare l’integrale in un opportuno intervallo si usa una tabella standard che lo calcola.
Ad esempio:
![]()
osservando la tabella allegata:
si deve trovare la riga corrispondente al valore ![]() e si nota che alla colonna 0.00 il valore è 0,8413.
e si nota che alla colonna 0.00 il valore è 0,8413.
Significa che la probabilità che un evento sia minore di 1 vale esattamente 84,13%.
Se avessi dovuto calcolare
![]()
mi sarei posto sempre sulla riga dell’1 ma alla colonna 0,01 e la probabilità sarebbe stata 0,8438 ossia in percentuale 84,38.
Ricapitolando la riga mi fornisce il valore della ![]() per un il valore intero seguito da un decimale e la colonna mi fornisce il valore corrispondente a partire dal secondo decimale.
per un il valore intero seguito da un decimale e la colonna mi fornisce il valore corrispondente a partire dal secondo decimale.
Passaggio dalla gaussiana normalizzata a quella standard attraverso la tabella fornita
Ma se un evento ha media ![]() e deviazione standard
e deviazione standard ![]() come faccio a collegarla alla gaussiana standard?
come faccio a collegarla alla gaussiana standard?
Devo calcolare la probabilità che il mio evento sia sempre minore di 3.
Allora dalla relazione:
![]()
andando a vedere la tabella si vede che vale 0,10 ossia il circa il 10%.
