Studiare il grafico di una funzione non è cosa assolutamente semplice, inoltre spesso non interessa il grafico completo ma solo il suo andamento in un intorno di un suo determinato punto.
Per fare questo è sufficiente avere un punto attorno il quale la funzione da approssimare sia derivabile n volte e si può approssimare la funzione di partenza con un polinomio.
Allora vale il seguente teorema fondamentale in analisi che consente l’approssimazione voluta.
Sia 
una funzione derivabile 
volte in 
allora si può approssimare la funzione di partenza con un polinomio tale che:
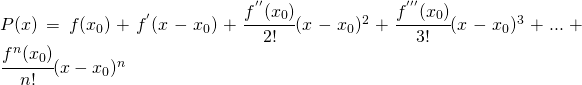
più ci si allontana dal punto e meno precisa è l’approssimazione polinomiale della funzione.
Se poi il punto 
lo sviluppo in serie precedente si chiama serie di McLaurin
