Salvador Dalì – “Afrodite”
La formula di sdoppiamento viene utilizzata per
DETERMINARE LA RETTA TANGENTE ALLA CIRCONFERENZA IN UN PUNTO CHE APPARTIENE ALLA CIRCONFERENZA
Eccola:
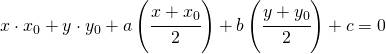
DIMOSTRAZIONE
L’equazione della circonferenza è:
(1) 
il punto 
appartiene alla circonferenza per cui è soddisfatta la seguente identità:
(2) 
Sottraggo la seconda alla prima e si ha:
(3) 
semplifico, sviluppo i due binomi tra parentesi come la differenza di binomi e raggruppo diventa:
(4) 
Considerando adesso che l’equazione della retta passante per il punto P ha equazione:
(5) 
sostituisco la (5) nella (4), quest’ultima diventa:
(6) 
posso dividere il tutto per 
e la (6) diventa:
(7) 
siccome il punto P appartiene a questa curva sostituendo le sue coordinate la (7) diventa:
(8) 
sviluppando le parentesi
(9) 
sommando i monomi uguali ho:
(10) 
risolvendola rispetto la variabile m:
(11) 
.
Ultimo passo è sostituire la (11) nell’equazione generica della retta (5) che diventa:
(12) 
facendo il m.c.m. ho:
(13) 
) sviluppando il prodotto dei binomi e portando tutto dalla stessa parte:
(14) 
riordinando i vari termini ho
(15) 
ora dalla (2) so che:
(16) 
sostituendola al binomio tra parentesi e sviluppando la moltiplicazione per 2 ho:
(17) 
e sommando i binomi risulta:
(18) 
dividendo per 2 tutti i monomi risulta la formula di sdoppiamento conosciuta:
(19)
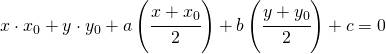
Formula che complica la vita agli studenti perchè costringe a imparare un mucchio di roba a memoria !!! Quale è il valore aggiunto rispetto al sistema retta / circonferenza e porre il delta a zero ?
La formula permette di trovare l’equazione della retta in tempi molto inferiori rispetto a quello del “sistema”. Inoltre esso è poi applicabile per ogni conica e l’intersezione con una retta. In certi casi, vedi esame di maturità, poi università e poi infine nel calcolo avanzato ingegneristico e non solo, tale metodo risparmia molti calcoli. Inoltre esso è molto valido nel caso anche si volesse implementare un algoritmo che possa dare immediatamente l’equazione della retta tangente con un programma.
Grazie comunque per la tua riflessione.
Dalla dimostrazione mi riamane comunque un dubbio,
per quale regola matematica ci è consentito di passare dal passaggio 2 a quello 3;
Perchè possimao eseguire la differenza tra l’ equazione della circonferenza con xp e yp e quella generale?
Buongiorno Giovanni,
come in tutte le equazioni, pensa ai sistemi di equazione ed al metodo della riduzione o dell’addizione, posso sempre sommare due equazioni trovandone una terza. Ad esempio, scrivendo a+b=0 e c+d=0 posso sempre scrivere a+b=0=c+d ossia a+b+c+d=0 ossia le ho sommate.
La condizione di tangenza è nel passaggio (6)->(7) esatto?
Ciao Adriano, in realtà nel passaggio (6) -> (7) ho raggruppato l’unico binomio presente nei tre membri, posso non considerarlo perchè quando x è uguale a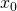
la retta degenera in un punto e quindi non riesco a determinare la m come puoi poi osservare nei passaggi successivi.
….’allora dove viene usata l ipotesi/condizione di tangenza?
Perché, seguendo la logica della dimostrazione, se si legge la dimostrazione e i vari passaggi, in questo modo sembra che qualsiasi retta (5) passante per P deve avere equazione (19)…. non so se mi sono spiegato….
Le rette che passano per un punto che appartiene sia alla circonferenza che alla retta stessa sono sempre tangenti. Non esplicito mai la condizione di tangenza ma la condizione di appartenenza che implica proprio la tangenza.
Adesso ho capito. Che passano per UN SOLO punto comune….
Ottimo, grazie per il confronto.