[:it]Retta tangente ad una curva in un punto appartenente alla curva stessa[:]

Pubblicato il 12 Settembre 2018 da admin

[:it]

Michael Khokhlachov

Dato un punto $P(x_{0},y_{0})$ , appartenente alla curva espressa da un’equazione $f(x,y)=0$ , la retta tangente avrà equazione:

$y=y_{0}-\frac{\cfrac{\delta f}{\delta x}\left ( x_{0},y_{0} \right )}{\cfrac{\delta f}{\delta y}\left ( x_{0},y_{0} \right )}\left ( x-x_{0} \right )$

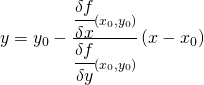
Tale relazione sostituisce, di fatto, le formule mnemoniche di sdoppiamento (ellisse , circonferenza) che normalmente si usano; come prerequisito, però, è la conoscenza della derivata di una funzione a due variabili.

Ad esempio:

Dato il punto di coordinate 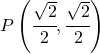$P\left (\cfrac{\sqrt{2}}{2},\cfrac{\sqrt{2}}{2} \right )$ e la circonferenza di equazione:

$x^2+y^2-1=0$

per determinare la retta tangente, per prima cosa calcolo:

$\cfrac{\delta f}{\delta x}=2x$

$\cfrac{\delta f}{\delta y}=2y$

inoltre:

$\cfrac{\delta f}{\delta x}\left ( \cfrac{\sqrt{2}}{2},\frac{\sqrt{2}}{2} \right )=2\cdot \cfrac{\sqrt{2}}{2}=\sqrt{2}$

$\cfrac{\delta f}{\delta y}\left ( \cfrac{\sqrt{2}}{2},\frac{\sqrt{2}}{2} \right )=2\cdot \cfrac{\sqrt{2}}{2}=\sqrt{2}$

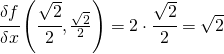
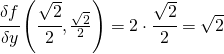
L’equazione della retta tangente diventa:

$y=\cfrac{\sqrt{2}}{2}-\cfrac{\sqrt{2}}{\sqrt{2}}\left ( x-\cfrac{\sqrt{2} }{2}\right )$

$y=\cfrac{\sqrt{2}}{2}-\left ( x-\cfrac{\sqrt{2} }{2}\right )$

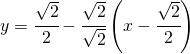
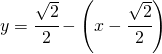
procedimento estremamente veloce efficace ed efficiente.[:]

Questa voce è stata pubblicata in Senza categoria. Contrassegna il permalink.

Lascia un commento Annulla risposta