
Igor Morski
Le disequazioni frazionarie sono indispensabili quando si tratta il segno di funzioni frazionarie. Esse sono utilizzate in molti campi a partire da quello economico come in quello della fisica.
Eccone un esempio:
![]()
Per risolverla si deve:
- studiare il segno del numeratore
- studiare il segno del denominatore
- rappresentare le soluzione sulla stessa retta orientata
- vedere il segno complessivo effettuando il prodotto.
NOTA importante:
nelle disequazioni frazionarie si studia sempre il numeratore maggiore o uguale a zero, il denominatore maggiore o uguale a zero e poi si considera il segno complessivo confrontandolo con il verso della disequazione di partenza.
Per capire il protocollo precedente sviluppo l’esercizio di partenza.
studio il numeratore
N:
![]()
![]()
studio il denominatore
D:
![]()
![]()
Li rappresento sulla retta orientata
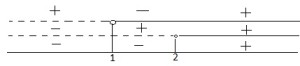 Studio la soluzione:
Studio la soluzione:
A destra del due ho una linea continua che significa che tutti i numeri a destra soddisfano il segno di maggiore.
A sinistra invece ho una linea tratteggiata che mi indica che tali numeri mi indicano che la disequazione è negativa.
Adesso noto che – per – fa più ossia in tale zona l’equazione frazionaria è positiva;
La soluzione diventa:
![]()
