![]()
Per risolverla devo avere la stessa base
Per fare questo utilizzo la seguente proprietà:
![]()
ossia:
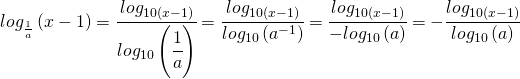
e
![]()
e inserendoli in quella di partenza ho:
![]()
e quindi facendo il m.c.m. la disequazione i di partenza diventa:
![]()
la disequazione di partenza è diventata:
![]()
Lo studio del dominio parte dall’argomento del logaritmo posto al numeratore:
![]()
ossia
![]()
il dominio diventa:
![]()
Adesso studio il segno del numeratore e del denominatore.
Il denominatore:
![]() >0
>0
E‘ positivo per
![]()
Mentre è negativo per
![]()
Il numeratore:
![]()
il -3 viene rappresentato con una linea tratteggiata.
![]() e quindi diventa
e quindi diventa
![]()
Concentrandosi solo sugli argomenti devo risolvere la seguente semplice disequazione:
![]()
quindi
![]()
Ho la seguente rappresentazione grafica:
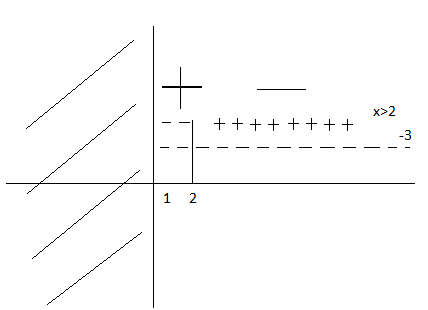
Adesso unisco il denominatore, che mi fornisce la dipendenza della disequazione dal parametro, ed il segno del numeratore.
Per
![]() il denominatore è positivo per cui ho il seguente schema:
il denominatore è positivo per cui ho il seguente schema:
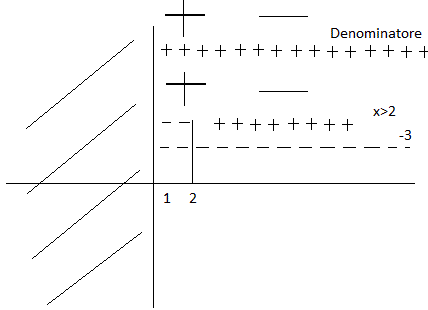
e quindi la prima soluzione è:
Per ![]()
![]()
Per ![]() il denominatore è negativo ed ho il seguente schema:
il denominatore è negativo ed ho il seguente schema:
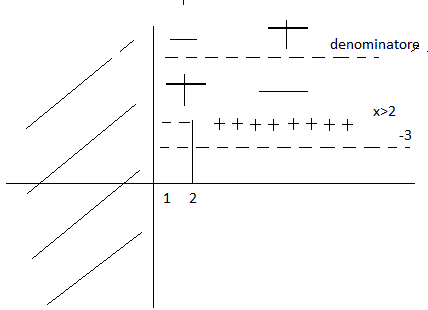
ed ho la seconda soluzione:
Per ![]()
![]()
