Ecco nuovamente il testo del problema:
![]() nel punto P(0;0)
nel punto P(0;0)
1- verifico che il punto appartenga alla curva:
![]()
risulta un’identità per cui il punto appartiene alla curva.
2- calcolo la derivata prima della curva.
![]()
sviluppando i calcoli
![]()
3- sostituisco l’ordinata del punto per trovare la m
![]()
l’equazione della retta tangente ha coefficiente angolare m=9 l’equazione della retta risulta
y=9x+q
Adesso sostituisco le coordinate del punto P
![]()
risolvendola rispetto all’incognita q
q=0.
La retta tangente alla curva ha equazione:
![]() .
.
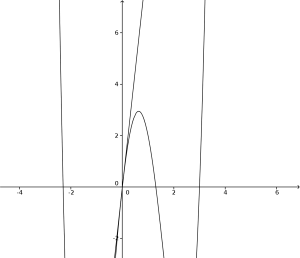
Graficamente la situazione si presenta in questi termini: