Le comunicazioni di tipo wireless fanno riferimento al protocollo 802.11. Nelle reti wired un indirizzo è messo in relazione con una postazione fissa.
In questo caso l’unità è una stazione (STA). Il livello fisico (PHY) è caratterizzato da:
- il mezzo utilizzato non ha limiti visibili ossia i frames di rete possono essere trasmessi anche se non si vede la STA
- non è protetto da segnali esterni
- la comunicazione è più dificoltosa
- si hanno topologie diverse di rete
- la comunicazione diretta tra STA non è in linea di massima possibile
- si hanno proprietà di comunicazione asimmetriche e tempo varianti.
802.11 si ha l’estensione della comunicazione da stazioni portabili a stazioni mobili.
Le stazioni mobili sono alimentate a batteria quindi per aumentare l’efficienza non si deve pensare ad usare una maggiore potenza del segnale.
ARCHITETTURA
Il servizio viene suddiviso in celle come accade per i servizi di telefonia mobile.
Ogni cella si chiama BBS (Basic Service Set) ed è controllata da un AC (Access Point).
Ogni AC è connessa attraverso una dorsale Ethernet ed anch’essa può essere di tipo wireless.
Si utilizza un Portal per consentire la connessione tra una rete LAN 802.11 ed una rete 802.
LIVELLO MAC – Data Link – Distributed Coordination Function
E‘ basato sul meccanismo di accesso multiplo con rilevamento della portante e prevenzione delle collisioni. (Carrier Sense Multiple Access con Collision Avoidance o CSMA/CA). I CSMA sono noti comunemente ma il più conosciuto è Ethernet.
CSMA: una stazione che desidera trasmettere ascolta il canale di comunicazione. Se è occupato la stazione rimanda la sua trasmissione all’istante successivo. Se invece è lbero allora la stazione può trasmettere.
Vi è la possibilità che due stazioni ascoltino il mezzo contemporaneamente e, pesando che sia libero, iniziano a trasmettere: in questo caso si ha una situazione di collisione.
Nel caso Ethernet, questa collisione viene gestita dalla stazione trasmettente usando un algoritmo chiamato Exponential Random Backoff Algorithm che fissa un tempo di ritrasmissione al termine del quale il canale viene nuovamente testato ed il tempo di ritrasmissione viene aumentato esponenzialmente.
Per le LAN questo metodo funziona perfettamente ma per il caso delle reti wired è da escludere perchè:
- la Collision Detection richiederebbe un ricetrasmettitore di tipo Full Duplex ossia trasmette e riceve contemporaneamente aumentando il prezzo degli apparati
- non possiamo assumere che tutte le stazioni si ascoltino a vicenda (ipotesi base per lo schema Collision Detection).
Il meccanismo che si adotta è il CA Collision Avoidance (CA) unito ad uno schema di Positive Acknowledge:
- una stazione ascolta il mezzo. Se il mezzo è occupato rinvia la trasmissione. Se il mezzo è libero in un intervallo di tempo chiamato DIFS) allora ha il permesso di trasmettere
- la stazione ricevente controlla il CRC (Cyclic Redundancy Checksums) del pacchetto ricevuto e manda un pacchetto di conferma (ACK). La ricezione della conferma denota che non si è verificata alcuna collisione. Comunque vene fissato un tempo massimo di ritrasmissione.
VIRTUAL CARRIER SENSE
Al fine di ridurre la probabilità che si verifichino collisioni tra due stazioni si usa il seguente meccanismo:
- si trasmette un pacchetto chiamato RTS (Request To Send) che include:
- sorgente e destinatario
- a durata della successiva trasmissione
la stazione destinatario risponde con un pacchetto di controlli di replica CTS (Clear to Send) che include le stesse informazioni.
Tutte le stazioni che ricevono RTS o CTS attivano il Virtual Carrier Sense (NAV Natowork Allocation Vector) per un certo periodo di tempo pari a quello indicato nel RTS o CTS.
Questo meccanismo riduce la probabilità di una collisione su un’area di ricezione che è nascosta all’interno dell’intervallo di tempo necessario alla trasmissione del pacchetto RTS. La durata della trasmissione protegge l’area del trasmettitore dalle collisioni.
RTS e CTS sono molto piccoli e vengono riconosciuti molto velocemente.
Fragmentation e Reassembly
In una rete locale si utilizzano pacchetti aventi dimensioni di diverse centinaia di Bytes (pacchetto Ethernet 1518 Bytes). Nel caso della comunicazione radiomobile i pacchetti sono di dimensioni molto minori:
- Bit Error Rate per un collegamento radio è molto elevata. La probabilità che la trasmissione di un pacchetto non vada a buon fine è proporzionale alla lunghezza.
- nel caso di un pacchetto alterato ho un overhead più piccolo (il tempo di ritrasmissione)
- in un sistema Frequency Hopping non è garantita la continuità del mezzo trasmissivo a causa dei salti di frequenza (avvengono ogni 20ms). Riducendo la dimensione del pacchetto diminuisce la probabilità che la trasmissione sia posticipata.
Comunque per consentire la trasmissione di grandi pacchetti si usa un algoritmo Send and wait:
- la stazione trasmittente non ha il permesso di trasmettere un nuovo pacchetto fono a che non si sia verificata:
- la ricezione di un ACK precedentemente trasmesso
- decide che il pacchetto è stato ritrasmesso troppe volte per cui si elemina l’itnero frame.
Lo standard permette alla stazione di trasmettere altri pacchetti (contenti altri indirizzi) prima di eseguire la ritrasmissione. Quindi un AP possiede vari pacchetti in uscita.
METODI DI ACCESSO AD UNA BSS
Quando una stazione vuole accedere ad una BSS esistente la stazione necessita di acquisire la sincronizzazione.
- Passive Scanning: la stazione aspettadi ricevereun Beacon Frame (frame spedito da AP per il sincronismo dei dati)
- Active Scanning : la stazione cerca l’access Point trasmettendo un Probe Request Frame .
PROCESSO DI AUTENTICAZIONE e DI ASSOCIAZIONE
AP e stazione di scambiano le password. I DSS ossia l’insieme dei AP sono informati circa la posizione della stazione e capire a quale BSS trasmettere.
ROAMING
E‘ il processo che consente lo spostamento di una stazione da una cella ad un’altra senza perdere la connessione.
- in una rete LAN la transizione da una cella all’altra deve avvenire tra la trasmissione del pacchetto e quello successivo.
- in un sistema telefonico, una disconnessione non influisce sulla trasmissione mentre in un sistema a pacchetti questo riduce le prestazioni.
Lo standard 802.11 non dice come deve essere implementato il roaming ma il funzionamento i base. Il processo di reassociazione consta di uno scambio di informazioni tra due AP interessati allo scambio attraverso il Distribution System senza appesantire la comunicazione attraverso il canale radio.
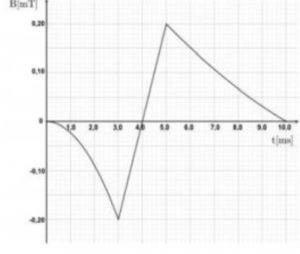
![]() racchiude un’area di
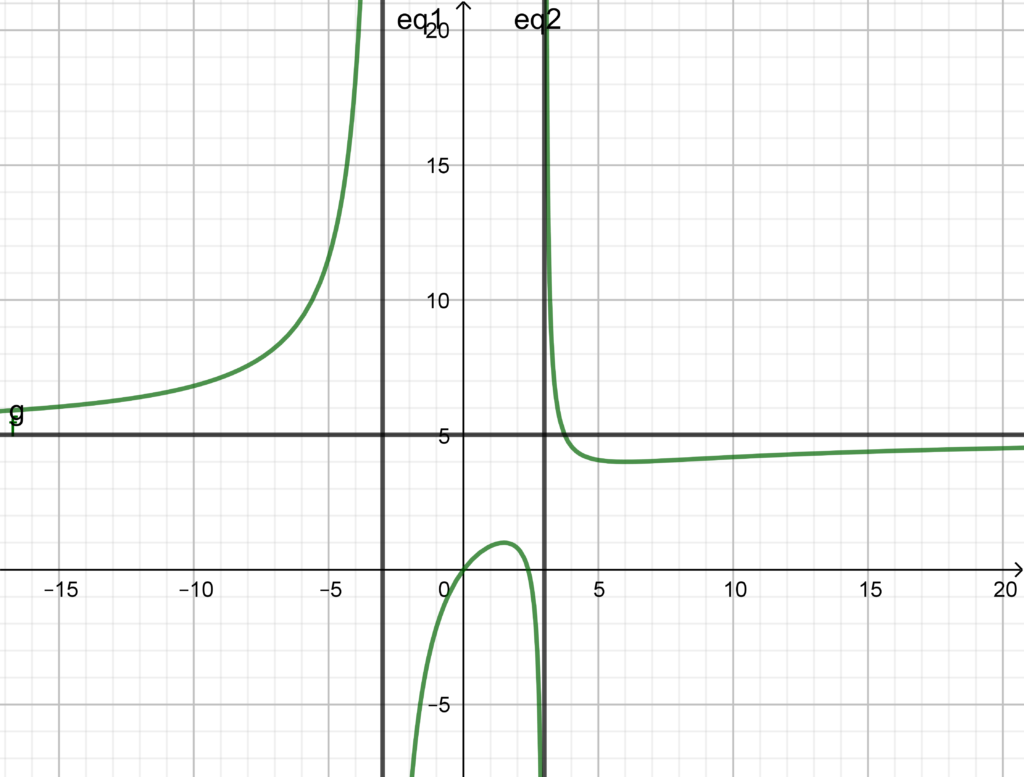
racchiude un’area di ![]() ed è immersa in un campo magnetico uniforme, le cui linee di forza sono perpendicolari alla superficie della spira. La component del campo magnetico perpendicolare alla superficie varia nel tempo come indicato in figura.
ed è immersa in un campo magnetico uniforme, le cui linee di forza sono perpendicolari alla superficie della spira. La component del campo magnetico perpendicolare alla superficie varia nel tempo come indicato in figura.![]()
![]()
![]()
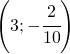 negli altri due casi sono delle rette che passano per i punti estratti dal grafico.
negli altri due casi sono delle rette che passano per i punti estratti dal grafico.![]()

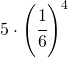
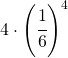
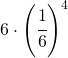
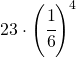
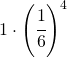
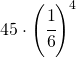
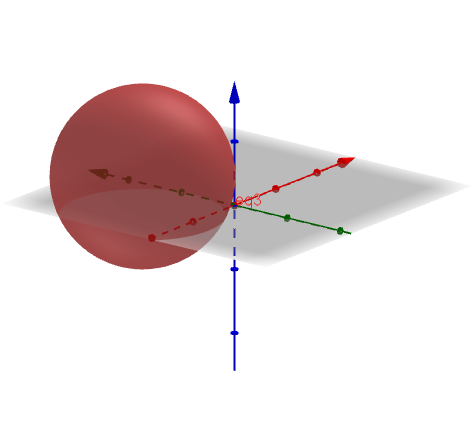
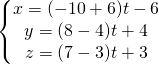
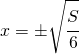
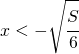 ed
ed 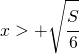
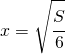
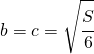
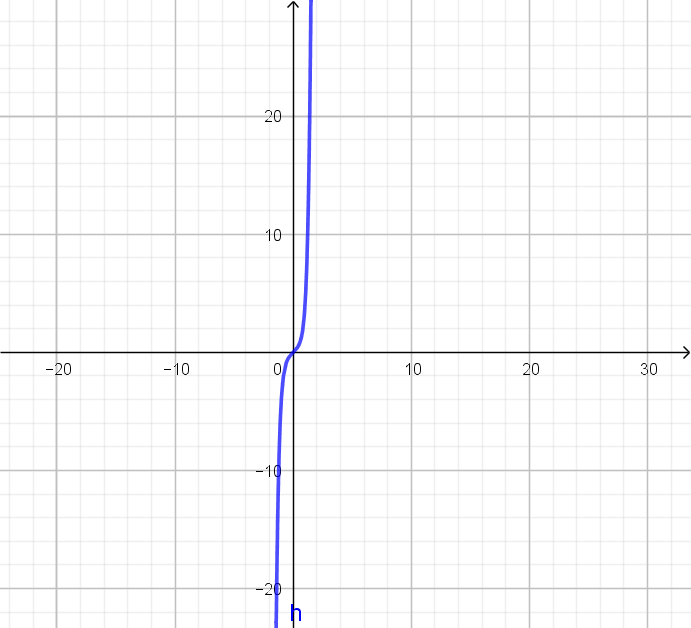
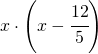 ; si deve inserire l’ulteriore condizione che è presente un asintoto orizzontale in
; si deve inserire l’ulteriore condizione che è presente un asintoto orizzontale in 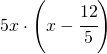 .
.