Maturità 2017: decimo quesito

Samy Charnine

Data la funzione

(1)  

verificare che essa non soddisfa tutte le ipotesi del teorema di Rolle nell’intervallo e che comunque esiste almeno un punto dell’intervallo [-3;3] in cui la derivata prima si annulla. Questo esempio contraddice il teorema di Rolle? Motivare la risposta in maniera esaustiva.

Prerequisiti

• conoscere il teorema di Rolle
• saper fare il grafico di una funzione con il modulo
• saper fare il grafico di una conica in maniera veloce

Sviluppo

Teorema di Rolle
Data una funzione definita in un intervallo limitato e chiuso con le seguenti proprietà:

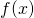• è continua in [a;b],
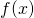• è derivabile in [a;b],
• ,

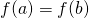Sviluppo la funzione (1)

la applico:

(2)  

essa rappresenta due parabole con intersezioni con l’asse x che valgono +2 e -2.
Il grafico è infatti:

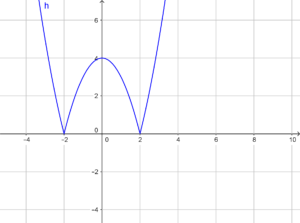
Il teorema di Rolle non è soddisfatto in quanto in -2 ed in 2 la funzione non è derivabile e sono due punti all’intervallo dell’intervallo [-3;3].
Non sono punti di derivabilità in quanto punti angolosi.

Ma se restringo l’intervallo, ad esempio[-1;1] il teorema di Rolle è perfettamente applicabile.
Infatti e tutte le altre condizioni dono soddisfatte.