Samy Charnine
Dimostrare che l’equazione:
(1) 
ha una e una sola soluzione reale
Prerequisiti
- conoscere il teorema di unicità dello zero
- calcolare la derivata
- calcolare un limite
- sapere la derivata delle funzioni trigonometriche
Sviluppo
Il teorema di unicità dello zero afferma che:
Se la derivata 
è non nulla in ogni punto di 
, la funzione ammette soltanto uno zero in tale intervallo aperto.
pongo
(2) 
Calcolo i seguenti due limiti:
(3) 
(4) 
effettuando adesso al derivata prima ho:
(5) 
La derivata prima è sempre positiva per cui la funzione di partenza è sempre crescente.
Le ipotesi del teorema sono soddisfatte e l’equazione ha una e una sola soluzione reale.
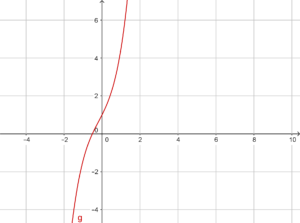
Il grafico di questa funzione è infatti:
