Alex Alemany
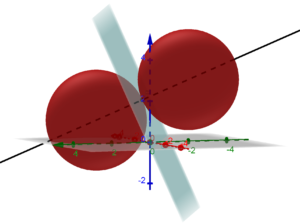
Determinare le coordinate dei centri delle sfere di raggio ![]() tangenti sl piano
tangenti sl piano ![]() di equazione:
di equazione:
(1) ![]()
nel suo punto ![]() di coordinate (1,0,2).
di coordinate (1,0,2).
Prerequisiti
- conoscere l’equazione della sfera nello spazio
- conoscere la formula che esprime la distanza di un punto da un piano
- conoscere l’equazione della retta passante per un punto e perpendicolare ad un piano
- conoscere la condizione di appartenenza di un punto ad una retta
Sviluppo
L’equazione di una retta passante per un punto in forma parametrica è:
(2) 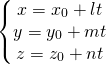
![]() ,
,![]() ,
,![]() , rappresentano le coordinate del vettore direzione
, rappresentano le coordinate del vettore direzione ![]() ossia quello parallelo alla retta.
ossia quello parallelo alla retta.
L’equazione generale di un piano ha equazione:
(3) ![]()
i coefficienti ![]() ,
,![]() e
e ![]() rappresentano le coordinate del vettore perpendicolare al piano.
rappresentano le coordinate del vettore perpendicolare al piano.
Unendo queste due richiami teorici la retta passante per ![]() e perpendicolare al piano
e perpendicolare al piano ![]() in forma parametrica è:
in forma parametrica è:
(4) 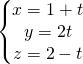
La formula della sfera è:
(5) ![]()
con ![]() centro della sfera ed
centro della sfera ed ![]() raggio della sfera.
raggio della sfera.
applicandola si ha:
(6) ![]()
Adesso richiamo la formula della distanza di un punto da un piano:
(7) ![]()
con ![]() i coefficienti del piano (3) e
i coefficienti del piano (3) e ![]() il punto P di cui si vuole conoscere la distanza dal piano stesso.
il punto P di cui si vuole conoscere la distanza dal piano stesso.
Applicandola sapendo che la distanza tra il centro ![]() e il piano
e il piano ![]() vale
vale ![]() :
:
(8) ![]()
Il centro ![]() appartiene alla retta trovata (4) per cui essa diventa:
appartiene alla retta trovata (4) per cui essa diventa:
(9) 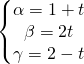
adesso esprimo ![]() in funzione delle coordinate del centro
in funzione delle coordinate del centro
(10) 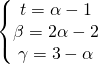
Adesso sostituisco i valori trovati nella (8) ed ho:
(11) 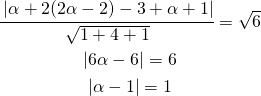
Sapendo che in generale
(12) ![]()
la applico:
(13) ![]()
quindi ho due equazioni:
(14) ![]()
e
(15) ![]()
i due centri hanno equazione:
(16) ![]()
e
(17) ![]()