Dati due piani:
![]()
![]()
PIANI PARALLELI
Quando le componenti del vettore ![]() e
e ![]() sono uno combinazione lineare dell’altro.
sono uno combinazione lineare dell’altro.
Ossia:
![]()
![]()
![]()
in maniera più compatta e semplice:
![]()
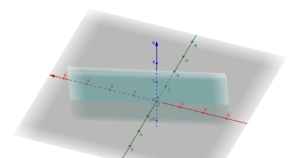
Ad esempio i piani:
![]()
![]()
sono paralleli come si vede nel grafico:
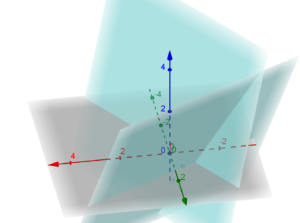
PIANI PERPENDICOLARI
Quando il prodotto scalare dei vettori ![]() e
e ![]() è nullo.
è nullo.
Il prodotto scalare è:
![]()
quando sono perpendicolari ![]()
e quindi la condizione è
![]()
Ad esempio i piani
![]()
![]()
sono perpendicolari infatti
![]()
e graficamente