Le parabole pure sono del tipo:
![]()
![]()
![]()
che più velocemente viene scritta come
![]()
Studio adesso quest’ultima.
Passo1: intersezioni con gli assi:
x=0
allora
y=0
ancora, se metto y=0
la x è ancora 0.
Passo 2: analisi della concavità
A=1
ossia la concavità è verso l’alto
Passo 3: coordinate del vertice
![]()
![]()
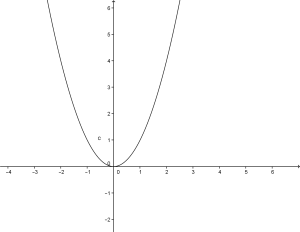
quindi li grafico risulta