Se ![]() è un numero primo allora
è un numero primo allora

![]()
equivalente a:
![]()
una sua conseguenza
![]()
equivalente a:
![]()
fondamentale che ![]() sia un numero primo!
sia un numero primo!
Esempi di sua applicazione
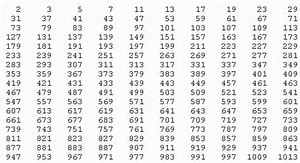
![]()
![]()
![]()

Se ![]() è un numero primo allora
è un numero primo allora

![]()
equivalente a:
![]()
una sua conseguenza
![]()
equivalente a:
![]()
fondamentale che ![]() sia un numero primo!
sia un numero primo!
Esempi di sua applicazione

![]()
![]()
![]()