Informatica – Unità di misura informatiche – connessione
|
You must specify a text. |
|
|
You must specify a text. |
|
|
You must fill out this field. |
|
|
You must specify a date. |
I tag HTML possono essere corredati di uno o più attributi, che servono per meglio specificare la funzione o la tipologia dell’elemento, per memorizzare dati o per arricchire di significato il contenuto.
Un tag con attributi si scrive in questo modo:
<tag attributo1=”valore1″ attributo2=”valore2″>
Ecco un esempio pratico:
<input type="email" name="email" placeholder="Scrivi il tuo indirizzo email..."> Il tag input indica genericamente un elemento che consente agli utenti di inserire delle informazioni. Grazie agli attributi però, possiamo specificare che vogliamo un indirizzo email (attributo type) e possiamo comunicarlo all’utente con un messaggio (attributo placeholder).
In sostanza gli attributi:
= (uguale);"", ma è possibile anche utilizzare gli apici '';Nota: in alcune rare situazioni, come quando il valore dell’attributo contiene in sè le virgolette, è necessario usare gli apici (es. data-nome = 'Luca "la roccia" Rossi').
Un malware infettivo è composto da poche righe di codice che si attaccano a un programma, infettandolo. Si installa automaticamente e lavora in background.
Il malware infettivo consiste, in linea di massima, di virus e worm.
La “vita” di un virus informatico si svolge in tre fasi: trasmissione, riproduzione e alterazione.
Worm: tradotto in lingua italiana “Verme“. Questo tipo di malware modifica il sistema operativo in modo da essere eseguito automaticamente ogni volta che viene acceso il sistema, rimanendo sempre attivo, fin quando non si spegne il computer. Si muove quindi senza bisogno di intervento esterno. È in grado di replicarsi come fa un virus, ma non ha bisogno di “attaccarsi” ad altri file eseguibili dato che usa internet per potersi riprodurre rapidamente e autonomamente. Uno dei mezzi per il contagio è la posta elettronica: il worm invia email ai contatti memorizzati allegando un file infetto (attachment). Per difendersi occorre tenere sempre aggiornato il sistema operativo.
Abbiamo visto che un malware si può introdurre in un computer in diversi modi. A seconda dei casi si può distinguere in:
Il termine Malware è l’abbreviazione di “malicious software“, software dannoso.
Malware è un qualsiasi tipo di software indesiderato che viene installato senza un adeguato consenso.
Lo scopo di un malware è creare danni al software (e hardware) del computer o ai dati dell’utente del pc:
Spesso si confonde il termine malware con virus.
Per malware si intende l’intera tipologia dei software dannosi.
Un virus è un tipo di malware che, come vedremo, ha la caratteristica di replicarsi infettando l’intero computer e quelli a cui sono collegati: un virus, per infettare il pc, necessita dell’intervento umano come il doppio clic di mouse su un file o su un’immagine in internet. Da quel momento darà inizio al contagio.
Un malware si può introdurre in un computer in vari modi. In generale i malware si diffondono tra i pc sfruttando i metodi di comunicazione esistenti. Ogni sistema adatto a trasportare informazioni da un pc a un altro è candidato a diventare sistema di infezione. È possibile infettare un computer attraverso una chiave USB, un cd o ogni altro strumento di memorizzazione rimovibile, oppure utilizzando le reti informatiche.
Attualmente i malware si diffondono soprattutto utilizzando le reti di computer, prima tra tutti internet, e la posta elettronica, sfruttando anche l’inesperienza di molti utenti e, nel caso delle mail, la curiosità. Gli utenti devono prestare attenzione soprattutto quando scaricano file e programmi da internet, soprattutto da siti poco conosciuti, e alle e-mail con allegati. Proprio le e-mail sono il metodo di diffusione principale dei malware, sfruttando “buchi” dei software di posta e la curiosità degli utenti che aprono qualsiasi messaggio arrivi sul PC, anche da indirizzi sconosciuti.
Se si protegge un documento, un foglio di calcolo, un file compresso con una password, per riaprire il documento è necessario fornire la password corretta. I dati cifrati non possono essere letti senza la chiave d’accesso e solo il proprietario o il destinatario autorizzato del file può leggere il messaggio.
Chiaramente è fondamentale che la password sia conservata dal proprietario in modo sicuro e che possa essere facilmente ritrovata dallo stesso in caso di bisogno.
La sicurezza dei dati protetti attraverso la crittografia dipende non solo sulla forza del metodo di crittografia, ma anche sulla forza della propria password, compresi fattori quali la lunghezza e la composizione della password e le misure che si prendono per assicurarsi che la password non sono comunicati a terzi non autorizzati.
I programmi di compressione permettono, tramite opportune tecniche, di ridurre le dimensioni dei file.
Esistono vari programmi di questo tipo: WinZip, WinRar,Tar.Gz, 7zip ecc.
Nel programma WinZip, nella versione dotata di funzioni di cifratura, selezionare Crittografa nella scheda Crea/Condividi.
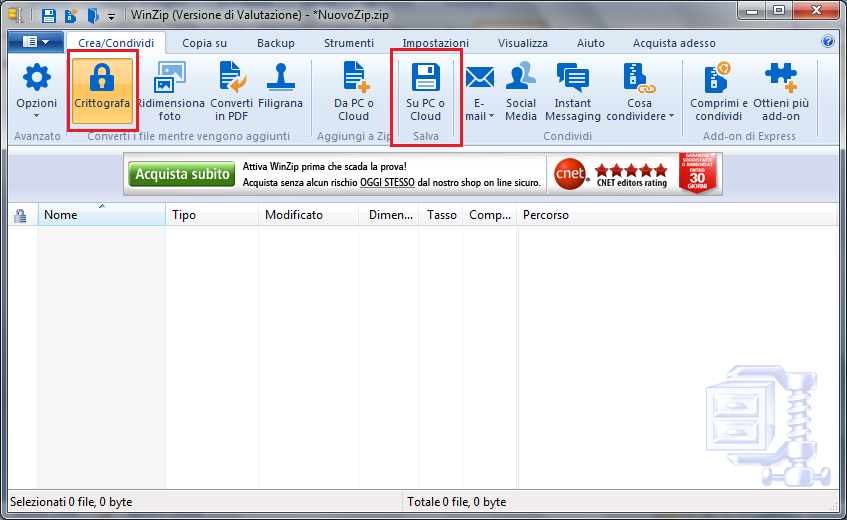
Sempre nella scheda Crea/Condividi fare clic sul pulsante Da Pc o Cloud per aggiungere a WinZip i file da comprimere.
Fare clic su Aggiungi. Dopo un avviso relativo ai vantaggi e svantaggi dei metodi di crittografia, appare la finestra per inserire la password.
Scegliere una password e reinserirla una seconda volta. Fare clic su OK. Quando si apre il file compresso appare la finestra di richiesta della password per decriptare il file.
È possibile proteggere un documento o un foglio di calcolo dall’apertura e/o dalla modifica mediante una password. Abbiamo già visto, nei capitoli precedenti, le caratteristiche che deve avere una password. Aggiungendo a un documento una password di apertura non sarà possibile aprirlo se non si digita la password corretta. Aggiungendo una password di modifica sarà possibile aprire il documento senza digitare la password, ma esso verrà aperto in sola lettura.
Per aggiungere una protezione mediante password a un documento o foglio di calcolo, per i programmi Microsoft Office, dal pulsante Office (versione 2007) o dal menu File (per la versione 2010), si sceglie il comando Salva, o Salva con nome se il documento era già stato salvato in precedenza.
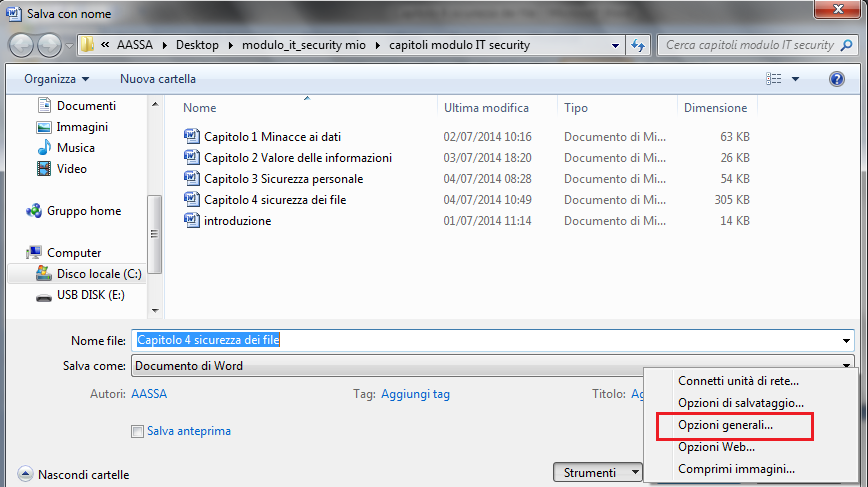
Dal menu Strumenti, selezionare la voce Opzioni generali. Appare la finestra per impostare le password di apertura e di modifica.
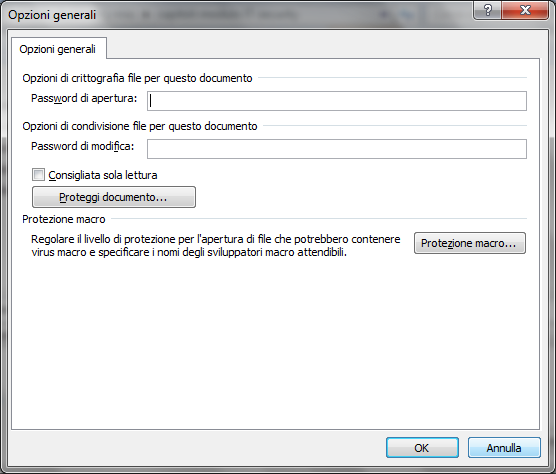
A questo punto si può digitare una password di apertura e/o una password di modifica del documento. Verrà richiesta la conferma delle password.
Eventualmente, si può selezionare la casella Consigliata sola lettura: in questo modo all’apertura del documento verrà visualizzato un messaggio che ne consiglia l’apertura in sola lettura. Se si modifica il documento aperto in sola lettura, sarà necessario salvarlo con un nome diverso. È possibile selezionare la casella Consigliata sola lettura senza impostare alcuna password.
Altre impostazioni di protezione sono presenti nel pulsante Office con la voce Prepara.
Scegliendo la voce Crittografa documento appare la finestra per inserire la password.
Il documento protetto da password viene crittografato con specifiche tecniche in modo che sia illeggibile da chi non è in possesso del codice di accesso.
Nel caso di software libero, come Libreoffice, la procedura per proteggere un documento è simile. Una volta aperto il file da proteggere, si sceglie Proprietà dal menu File.
Nella scheda Sicurezza fare clic sul pulsante Proteggi.
A questo punto si può inserire e confermare la password da applicare. Si può impostare la protezione con password anche con il comando Salva con nome.
Attivare/disattivare le impostazioni di sicurezza delle macro.
Una macro è un insieme d’istruzioni che il computer interpreta una dopo l’altra e traduce in azioni operative, né più né meno come se fossero state impartite manualmente da noi. Una macro può essere eseguita indefinitamente tutte volte che si desidera, e pertanto si rivela una ottima soluzione per automatizzare una volta per tutte l’esecuzione di procedure ricorrenti. Le applicazioni pratiche delle macro sono solo da immaginare: la stampa di una tabella, la formattazione di un documento, la creazione di un grafico, la ricerca di particolari valori, ecc.
Le macro, nel caso delle applicazioni Microsoft Office come Word, Excel, Access, sono scritte nel linguaggio Visual Basic for Application (VBA).
La sua funzione è quella di rendere programmabili questi applicativi, allo scopo di personalizzarli a seconda delle esigenze specifiche dell’utente.
Le macro generate per un file sono parte integrante del file. Il sistema operativo Windows visualizza l’icona dei file con macro in modo diverso dagli altri.
Hanno un punto esclamativo che le contraddistingue e un’estensione diversa (xlsm).
Abbiamo già visto che l’icona di un file con macro presenta un punto esclamativo, per porre attenzione sulla diversità rispetto ai file “normali”.
Quando si apre un file con macro il programma ci avvisa della presenza di questo codice con un avviso di protezione nella barra di notifica.
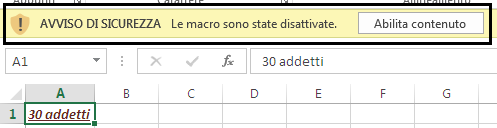
programmi Office, per impostazione predefinita, disattivano le macro presenti in un file. È una questione di sicurezza. Non conoscendo a priori il contenuto delle macro presenti, se sono “sicure” o se è codice “pericoloso” (per questo l’icona del file ha il segnale di attenzione) scritto per creare dei danni, si decide di disabilitare il codice.
Se si è sicuri del contenuto della macro, ad esempio perché è stata scritta dal proprietario del file, si può abilitare il codice con il pulsante Opzioni.
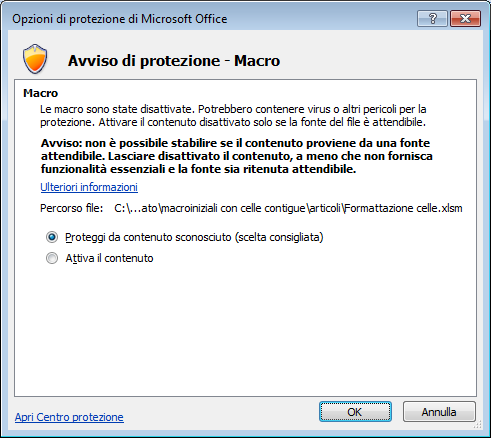
Le macro abilitate possono essere eseguite, Chiaramente, nel caso di macro di provenienza non nota o se l’autore delle macro non è attendibile, questa esecuzione potrebbe comportare dei danni al computer.